Flexible Neural Representation for Physics Prediction

Humans have a remarkable capacity to understand the physical dynamics of objects in their environment, flexibly capturing complex structures and interactions at multiple levels of detail. Inspired by this ability, we have developed a hierarchical particle-based object representation that covers a wide variety of types of three-dimensional objects, including both arbitrary rigid geometrical shapes and deformable materials. In this representation we learn to predict physical dynamics with an end-to-end differentiable neural network based on hierarchical graph convolution. We are able to generate plausible dynamics predictions at long time scales in novel settings with complex collisions and nonrigid deformations. Our approach has the potential to form the basis of next-generation physics predictors for use in computer vision, robotics, and quantitative cognitive science.

Further reading: Technical Tutorial and Implementation Details, FleX ML Agents Simulation Environment

Humans efficiently decompose their environment into objects, and reason effectively about the dynamic interactions between these objects. Although human intuitive physics may be quantitatively inaccurate under some circumstances, humans make qualitatively plausible guesses about dynamic trajectories of their environments over long time horizons. Moreover, they either are born knowing, or quickly learn about, concepts such as object permanence, occlusion, and deformability, which guide their perception and reasoning.

An artificial system that could mimic such abilities would be of great use for applications in computer vision, robotics, reinforcement learning, and many other areas. While traditional physics engines constructed for computer graphics have made great strides, such routines are often hard-wired and thus challenging to integrate as components of larger learnable systems. Creating end-to-end differentiable neural networks for physics prediction is thus an appealing idea.

Recent work has illustrated the use of neural networks to predict physical object interactions in (mostly) 2D scenarios by proposing object-centric and relation-centric representations. Common to these works is the treatment of scenes as graphs, with nodes representing object point masses and edges describing the pairwise relations between objects (e.g. gravitational, spring-like, or repulsing relationships). Object relations and physical states are used to compute the pairwise effects between objects. After combining effects on an object, the future physical state of the environment is predicted on a per-object basis.

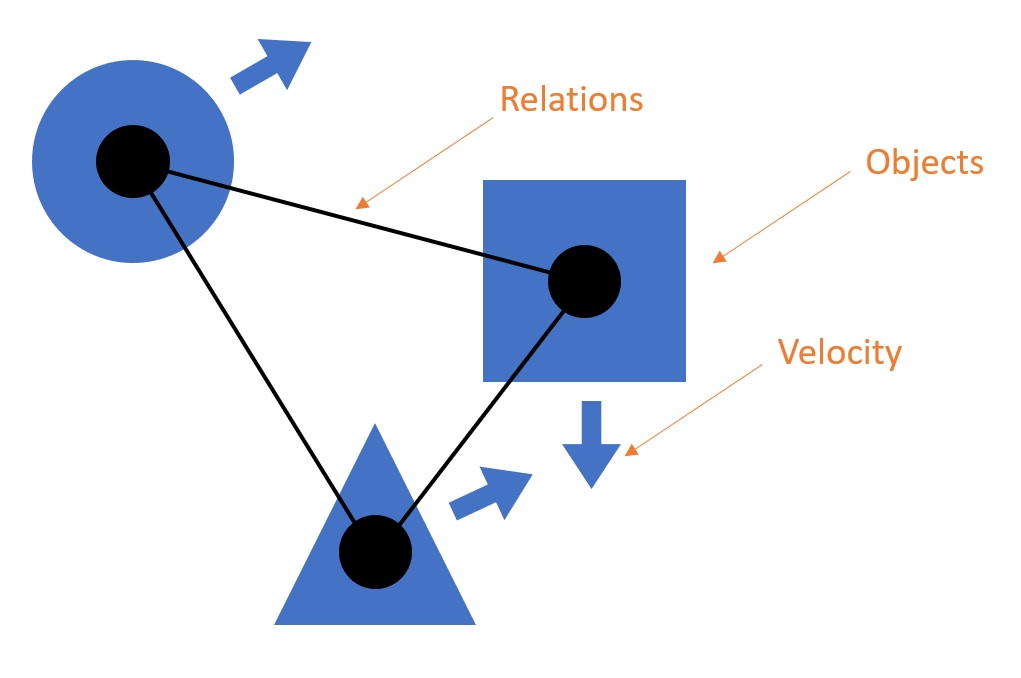
This approach is very promising in its ability to explicitly handle object interactions. However, a number of challenges have remained in generalizing this approach to real-world physical dynamics, including representing arbitrary geometric shapes with sufficient resolution to capture complex collisions, working with objects at different scales simultaneously, and handling non-rigid objects of nontrivial complexity.

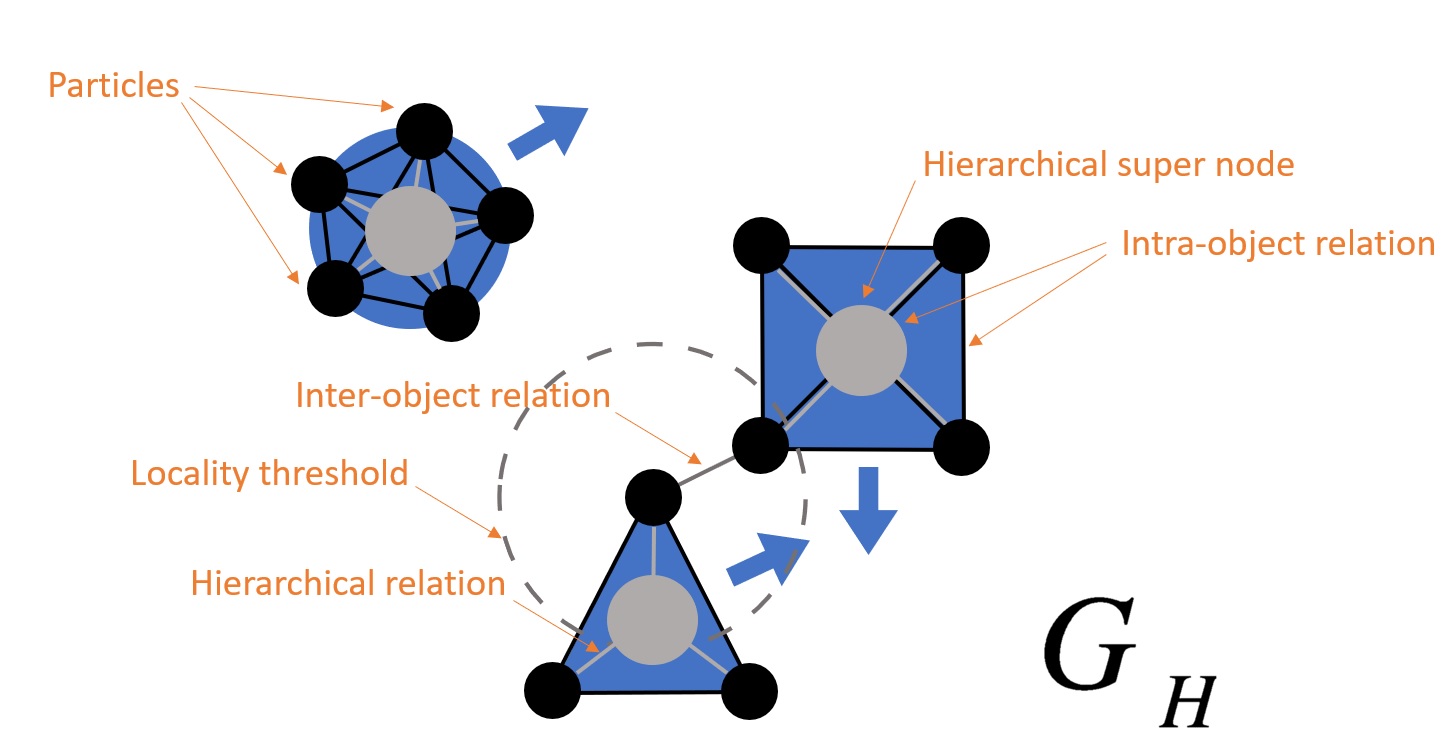
As a solution to these issues, we propose a novel cognitively-inspired hierarchical graph-based object representation that captures a wide variety of complex rigid and deformable bodies, and an efficient hierarchical graph-convolutional neural network that learns physics prediction within this representation.

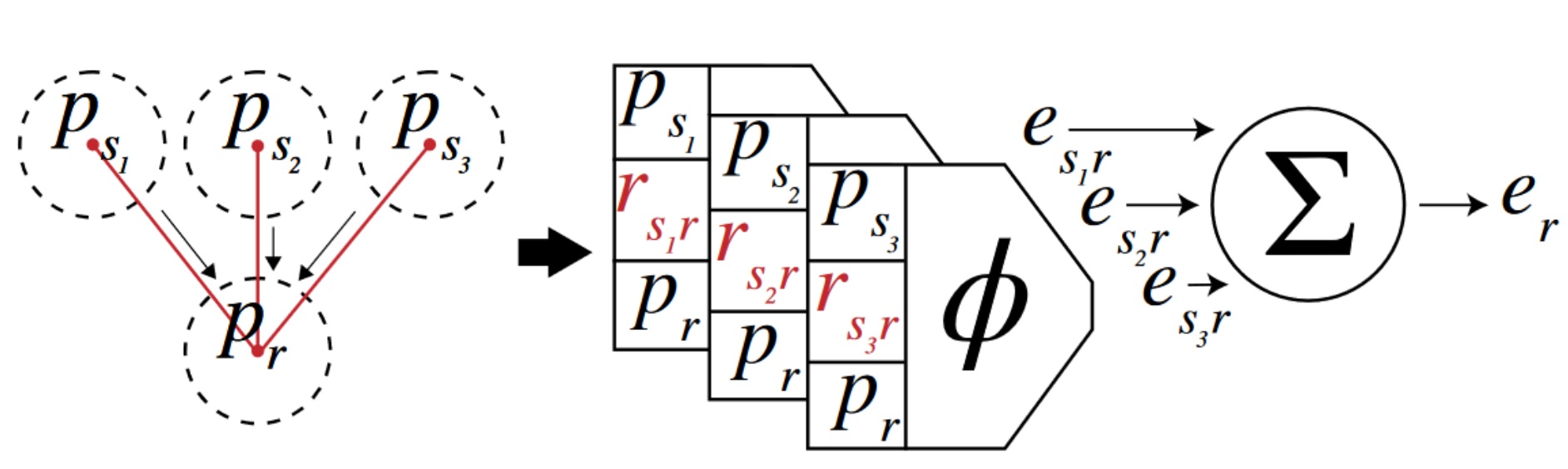
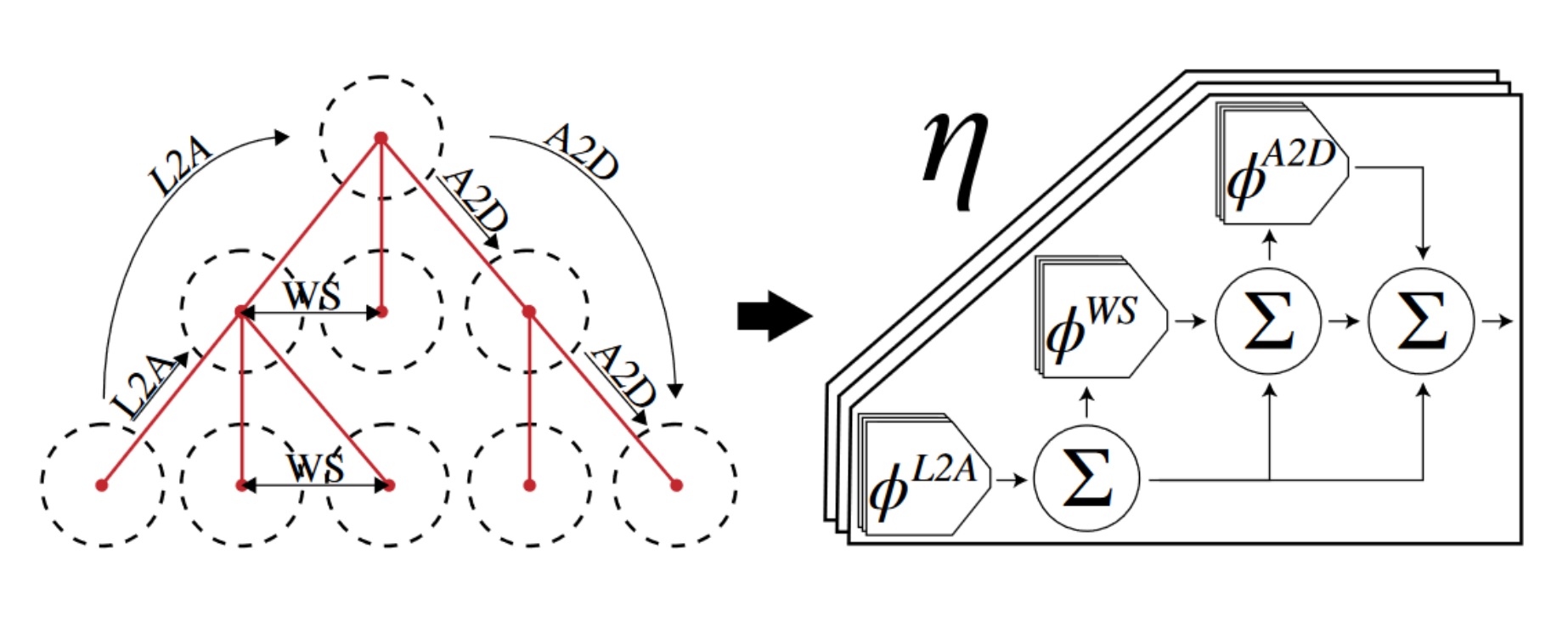
Before we get to the full architecture of the Hierarchical Relation Network (HRN), let’s first introduce two main components of the model. The first is pairwise graph convolution, which is composed of two parts: (1) A pariwise processing unit Φ that takes the sender particle state p_s, the receiver particle state p_r, and their relation r_sr as input and outputs the effect e_sr of p_s on p_r, and (2) a commutative aggregation operation Σ which collects and computes the overall effect e_r. In our case, this is a simple summation over all effects on p_r.

Pairwise processing limits graph convolutions to only propagate effects between directly connected nodes. For a generic flat graph, we would have to repeatedly apply this operation until the information from all particles has propagated across the whole graph. This is infeasible in a scenario with many particles. Instead, we leverage direct connections between particles and their ancestors in our hierarchy to propagate all effects across the entire graph in one model step. We introduce the hierarchical graph convolution, a three stage mechanism for effect propagation.

The HRN takes the past particle graphs G^(t-T,t]_H = <P^(t-T,t], R^(t-T,t]> as input and outputs the next states P^t+1. The inputs to each graph convolutional effect module Φ are the particle states and relations, the outputs are the respective effects, for past states, collisions, and external forces. The hierarchical graph convolutional module η takes the sume of all effects, the pairwise particle states, and relations and propagates the effects through the (hierarchical) graph. Finally, Ψ uses the propagated effects to compute the next particle states P^t+1.

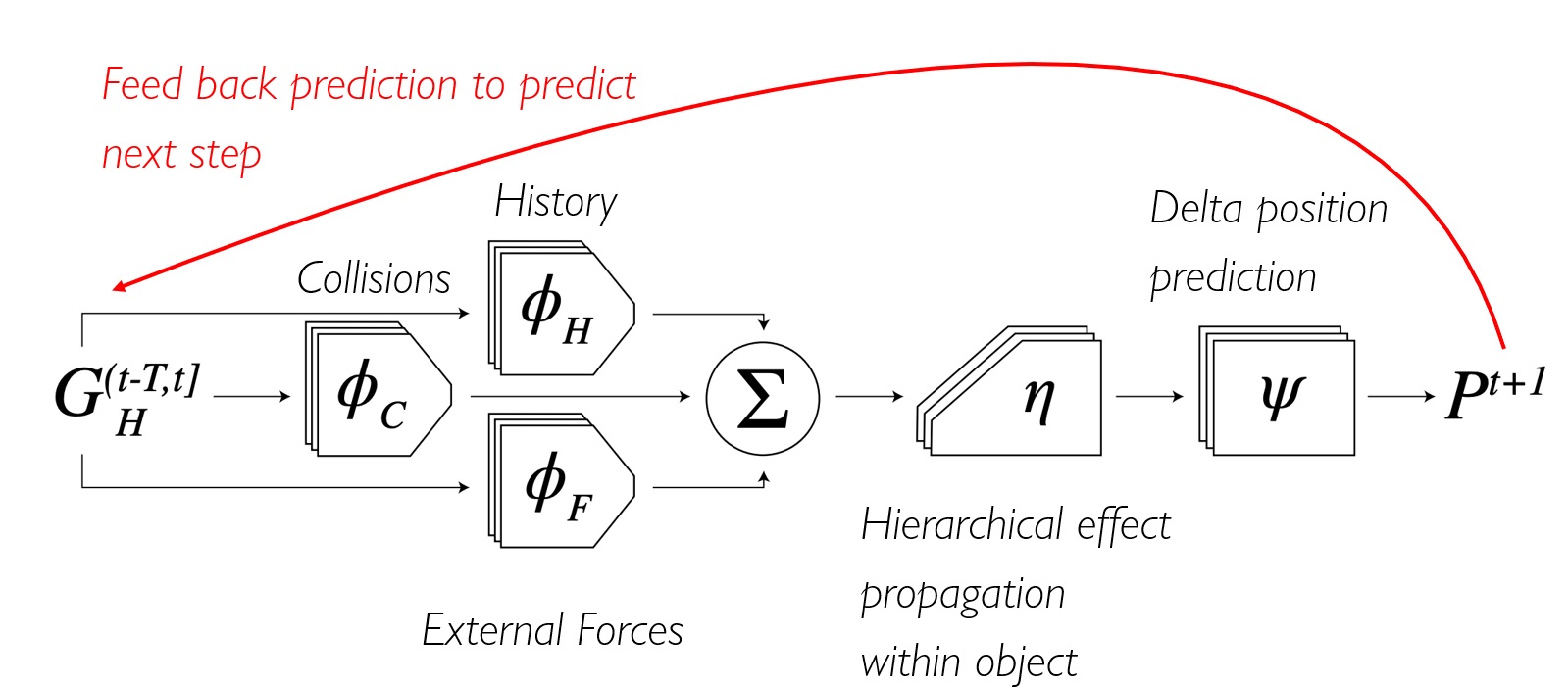
In order to get more accurate predictions, we leverage the hierarchical particle representation by predicting the dynamics of any given particle within the local coordinate system originated at its parent. This local position change relative to the parent is then used to compute one part of the loss term, the local loss. We also require that the future global delta position is accurate, the global loss. Finally, we aim to preserve the intra-object particle structure by imposing that the pairwise distance between two connected particles in the next time step matches the ground truth, the preservation loss. The final objective that is optimized for is a linear combination of these three terms.

Here we show some frame-by-frame predictions of our model versus the ground truth.

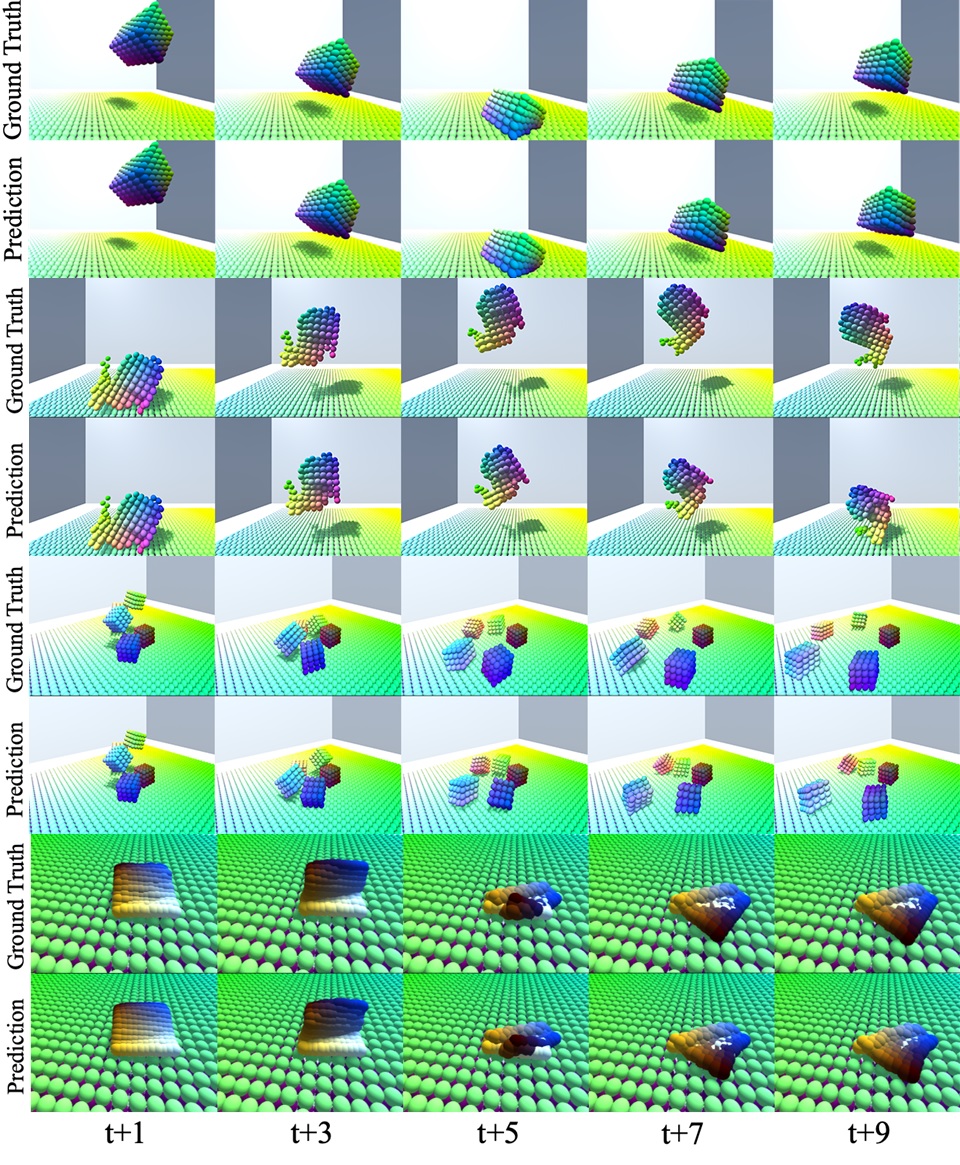
For more results, please check out the video which showcases the predictions of our model in many scenarios:

For an introduction into the physics prediction Tensorflow code that reproduces the results of our paper have a look at the technical tutorial in case you want to simulate and train from your own FleX scenes with different materials such as rigid bodies, soft bodies, cloth, inflatables, fluids or gases.

Thanks so much for reading. Please check out our paper and code repository for more and do not hesitate to contact us if you have any questions!

To cite our paper please use:

@inproceedings{mrowca2018flexible,
  title={Flexible Neural Representation for Physics Prediction},
  author={Mrowca, Damian and Zhuang, Chengxu and Wang, Elias and Haber, Nick and Fei-Fei, Li and Tenenbaum, Joshua B and Yamins, Daniel LK},
  booktitle={Advances in Neural Information Processing Systems},
  year={2018}
}

Further reading: Technical Tutorial and Implementation Details, FleX ML Agents Simulation Environment